摘要:,结构动力计算是结构力学领域的关键研究之一,特别是在数值积分法的应用上取得了显著进展。本文综述了结构动力响应的数值求解方法,重点讨论了目前结构动力学研究中的最新进展。介绍了几种主要的数值积分方法,如有限元法(FEM)、有限差分法(FDM)和离散元法(DEM),并比较了它们的适用性和优缺点。探讨了现代计算机技术在结构动力分析中的应用,包括高性能计算平台和并行计算技术,这些技术显著提高了计算效率和精度。概述了结构动力响应的最新研究成果,涉及新型材料、新型连接方式以及复杂几何形状对结构动态性能的影响。本文总结了结构动力计算的发展趋势,并对未来研究方向进行了展望。

一、结构动力学概述
- 定义:结构动力学是研究结构在动力荷载作用下的响应、性能及其设计方法的学科,主要研究结构的振动特性、动力响应、稳定性以及在动力环境中的优化设计等方面。
- 研究内容
- 结构在动力荷载下的响应,如位移、速度、加速度和应力等。
- 结构的振动特性,像固有频率、阻尼比和模态形状等,这些特性决定了结构对动态载荷的敏感度和响应特性。
- 结构在动力环境中的稳定性研究。
- 结构在动力环境下的优化设计。
- 研究方法
- 解析法:通过数学物理方程求解结构的动力响应,能得到精确解,但仅适用于简单结构和特定边界条件。
- 数值法:利用计算机进行数值模拟,例如有限元法、有限差分法、离散元法等,适用于复杂结构和各种边界条件。
- 实验法:通过动力试验验证理论模型和数值方法的正确性,为结构动力学研究提供直观依据。
二、结构动力计算基本原理
- 动力平衡方程
- 定义:是描述结构在动力荷载作用下,内力和外力之间平衡关系的数学表达式。
- 建立:根据牛顿第二定律,结合结构的运动微分方程,可以推导出结构的动力平衡方程。
- 应用:通过求解动力平衡方程,可以确定结构在任意时刻的位移、速度和加速度,进而求得结构的内力分布和动力响应。
- 达朗贝尔原理
- 定义:将动力学问题转化为静力学问题进行处理的基本原理,通过在质点上施加惯性力,将动力学问题等效为静力学问题求解。
- 应用:在应用时,需要将结构的惯性力和外力一并考虑,通过构建等效静力系,实现对结构动力响应的求解,适用于线性、小变形情况下的结构动力分析。
- 局限性:对于非线性、大变形问题则需要采用其他方法进行处理。
- 哈密顿原理
- 定义:基于变分法的一种结构动力分析方法,通过建立结构的拉格朗日函数,并寻求该函数的最小值,得到结构的运动方程。
- 优点:具有普适性,适用于线性和非线性、小变形和大变形等各种情况下的结构动力分析。
- 应用步骤:首先构建结构的拉格朗日函数,然后根据最小作用量原理建立运动方程,最后通过数值方法进行求解。
三、结构的模态分析
- 无阻尼自由振动
- 定义:结构在没有外部激励和阻尼影响下的自由振动状态。
- 性质:是一种简谐振动,其振幅和频率都是常数,且不随时间变化。
- 求解方法:通过结构的模态分析,可以得到结构的固有频率和振型,从而求解无阻尼自由振动的响应。
- 有阻尼自由振动
- 定义:其振幅随时间逐渐减小,最终趋于零,而频率也略有变化。
- 性质:与无阻尼自由振动有明显区别,考虑了阻尼因素对振动的影响。
- 求解方法:一般采用复模态分析法,得到结构的复频率和复振型,进而求解有阻尼自由振动的响应。
- 试验方法:试验内容包括结构的固有频率、振型、阻尼比等模态参数的测量。一般采用激振器对结构进行激励,通过测量结构响应的加速度、速度和位移等参数,经过数据处理和识别算法得到结构的模态参数。
四、结构动力响应计算
- 单自由度体系的强迫振动
- 强迫振动定义:单自由度体系在外部激励下的振动。
- 振动方程:根据牛顿第二定律建立单自由度体系的振动方程。
- 频率响应函数:描述体系振幅和相位与外部激励频率关系的函数。
- 阻尼对振动的影响:涉及阻尼比、自然频率与体系的振幅、相位关系的详细解释。
- 多自由度体系的强迫振动
- 多自由度体系模型:通过模态分析求解多自由度体系的自振频率和振型。
- 模态分析:将物理坐标转换为模态坐标,以解耦多自由度体系的振动方程。
- 坐标转换:利用模态叠加法求解多自由度体系在外部激励下的振动响应。
- 数值积分法求解结构动力响应
- 数值积分法概述:介绍求解结构动力响应的数值积分法,如Newmark - beta法、Wilson - theta法等。
- 逐步积分格式:详细推导数值积分法中的逐步积分格式,包括加速度、速度和位移的更新公式。
- 算法稳定性与精度:分析数值积分法的稳定性和精度,讨论积分参数的选择。
- 算例与应用:通过具体算例展示数值积分法在结构动力响应计算中的应用。
五、结构抗震设计动力计算
- 结构动力模型建立:要准确的建立结构动力模型,需要考虑结构的质量、刚度和阻尼分布,以及构件的连接方式和边界条件。
- 地震动特性:地震动具有随机性、非平稳性和多维性,对结构产生复杂动力效应。
- 地震动输入:根据地震危险性分析和场地条件,合理确定地震动输入,包括加速度、速度和位移时程。
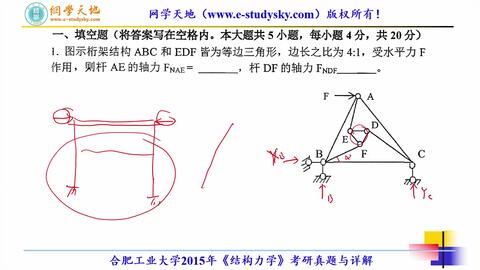
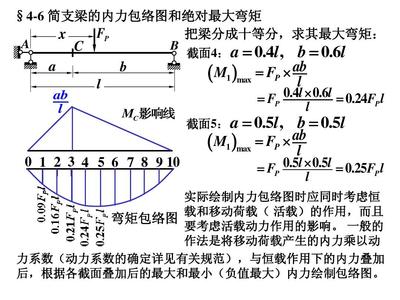
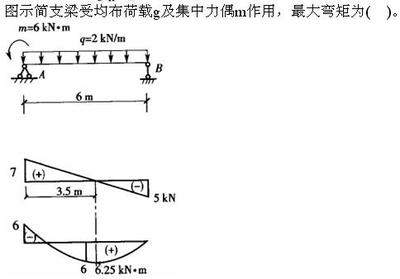
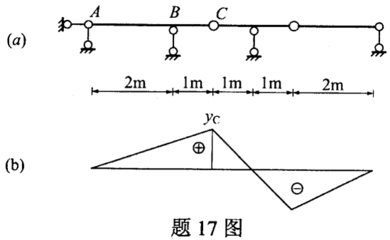
结构动力学在工程中的应用案例
动力荷载作用下的结构优化设计
结构动力计算的数值模拟技术
结构动力学研究的最新进展



