本文旨在对比有限元法和简易算法在考虑次应力的桁架结构计算中的效果。通过分析两种方法在处理复杂几何形状和材料非线性问题时的表现,发现尽管有限元法在精度上具有优势,但计算成本较高且对计算资源要求大。相比之下,简易算法虽然在精度上有所降低,但其计算速度快,适用于快速原型设计和初步设计阶段。建议根据具体应用场景选择适合的计算方法。
一、基于有限元法的桁架次应力计算技巧
- 计算思路方面
- 把结构剖分为一系列离散单元,即将具有无限多个自由度的连续体化为有限多个自由度的计算模型。例如在分析桁架结构时,将桁架看作是由多个单元组成的整体,每个单元有自己的特性和连接关系。然后选择一个表示单元内位移随位置变化的模式,并且按函数插值理论将单元任意一点的位移通过一定的函数关系用节点位移来表示。从分析单个单元入手,用变分原理建立单元方程,再把所有单元集合起来,并与节点上的外荷载相联系,进行整体的结构分析,得到一组以节点位移为未知量的方程,引入边界条件即可求解方程得到位移,最后根据几何方程和物理方程求得应力和应变。这种方法在计算桁架次应力时,能较为准确地模拟实际桁架结构的受力情况和应力分布情况,使次应力显示得更加明显。像在计算实际桁架结构,杆件的弹性模量、矩形截面的惯性矩、矩形截面面积,集中荷载作用于节点等情况时,可以利用有限元软件(如ANSYS)进行模拟计算,通过设定好各个参数和条件,得到较为准确的次应力结果。不过有限元法对电脑要求较高,对于大型和庞大的结构需要占用大量的电脑内存,对小型、简单的模型有时比较烦琐,比直接生成方法需要更多数据,在某些条件下可能会失败,即程序不能生成有限元网格。
- 结果准确性方面
- 有限元法计算精度高,是现在主流的计算软件。例如在一个桁架结构的计算实例中,用ANSYS法计算桁架结构中杆件的次应力,其计算结果和其他方法(如简易算法)对比,相对误差最大值为0.029%,能满足工程要求。在计算实际桁架结构时,可以通过调整节点的几何性能(如拖拉、旋转等几何操作)来模拟不同的实际情况,进而得到不同条件下的次应力结果,但要注意操作对电脑性能的要求。
二、简易算法的桁架次应力计算技巧
- 计算理论方面
- 简易算法主要是基于对结构力学中转角位移方程的应用。由于理想桁架产生次应力的根本原因是节点刚性,所以可以将理想桁架结构中的杆单元处理成梁单元进而得到次应力。在按梁单元去计算杆端弯矩时,对于转角是忽略的,因为节点刚性的影响效果毕竟是有限的,转角对于节点的位移来说就是高阶微量。在得知梁单元的杆端位移之后就可以利用转角位移方程求出各个梁单元的杆端弯矩,其中的杆端实际位移可以通过理想桁架铰接去计算得到,同时桁架结构的节点处的不平衡力矩就可以求得,再进行一次力矩分配,那么就可以既简单又方便地求出桁架结构次应力。例如在简单的桁架结构模型计算中,可以将桁架结构中的杆单元当作梁单元进行计算,通过已知的刚架结构MATLAB代码去处置桁架结构中的杆单元,即将杆单元处理成梁单元从而得到桁架结构的次应力。这种简易算法由于计算过程简单,相比ANSYS法更具有工程应用前景。
- 计算效率方面
- 简易算法计算过程相对简单,不需要像有限元法那样处理大量的单元和复杂的计算过程。在工程应用中,如果对精度要求不是极高的情况下,可以快速地得到桁架次应力的近似结果,从而节省计算时间和计算资源。

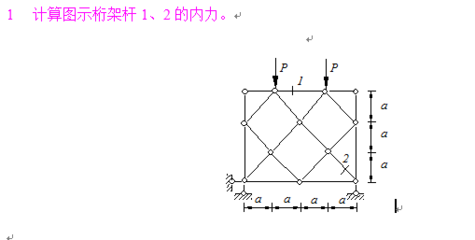

桁架次应力简易算法案例分析
有限元法与简易算法对比研究
ANSYS软件在桁架分析中的应用
桁架次应力计算的误差控制方法
桂林加固改造设计公司于2025-02-27回复
考虑次应力的桁架计算技巧,能够精确预测结构在复杂载荷下的响应,确保设计既安全又经济。
大连加固改造设计公司于2025-02-27回复
在桁架结构分析中,考虑次应力的计算技巧是确保结构安全的关键,有限元法提供了精确且全面的计算框架,而简易算法虽简化了问题,却可能在精度上有所妥协。



